hernández verón miguel ángel (12 Ergebnisse)
Suchfilter
Produktart
- Alle Product Types
- Bücher (12)
- Magazine & Zeitschriften (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Comics (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Noten (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Kunst, Grafik & Poster (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Fotografien (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Karten (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Manuskripte & Papierantiquitäten (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
Zustand Mehr dazu
- Neu (11)
- Wie Neu, Sehr Gut oder Gut Bis Sehr Gut (1)
- Gut oder Befriedigend (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Ausreichend oder Schlecht (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Wie beschrieben (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
Einband
- alle Einbände
- Hardcover (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Softcover (11)
Weitere Eigenschaften
- Erstausgabe (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Signiert (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Schutzumschlag (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- Angebotsfoto (7)
Sprache (2)
Preis
- Beliebiger Preis
- Weniger als EUR 20 (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
- EUR 20 bis EUR 45
- Mehr als EUR 45
Gratisversand
- Kostenloser Versand nach USA (Keine weiteren Ergebnisse entsprechen dieser Verfeinerung)
Land des Verkäufers
Verkäuferbewertung
-
Mild Differentiability Conditions for Newton's Method in Banach Spaces (Frontiers in Mathematics)
Verlag: Springer (India) Private Limited, 2020
ISBN 10: 3030487016 ISBN 13: 9783030487010
Sprache: Englisch
Anbieter: Majestic Books, Hounslow, Vereinigtes Königreich
EUR 48,15
EUR 7,40 für den Versand von Vereinigtes Königreich nach USAAnzahl: 1 verfügbar
In den WarenkorbZustand: New.
-
EUR 58,60
EUR 11,38 für den Versand von Vereinigtes Königreich nach USAAnzahl: 1 verfügbar
In den WarenkorbPaperback. Zustand: Brand New. 254 pages. 9.44x6.61x9.45 inches. In Stock.
-
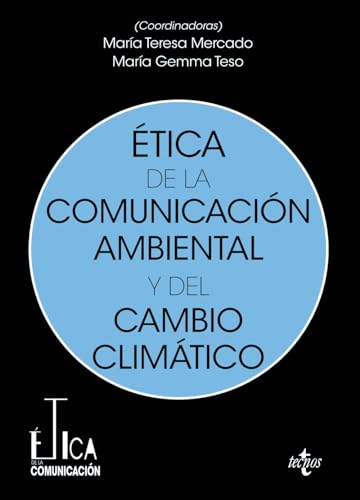
Ética de la comunicación ambiental y del cambio climático
Anbieter: KALAMO BOOKS, Burriana, CS, Spanien
Rústica Hilo. Zustand: Nuevo.
-
Mild Differentiability Conditions for Newton's Method in Banach Spaces
Anbieter: Revaluation Books, Exeter, Vereinigtes Königreich
EUR 84,97
EUR 11,38 für den Versand von Vereinigtes Königreich nach USAAnzahl: 2 verfügbar
In den WarenkorbPaperback. Zustand: Brand New. 192 pages. 9.45x6.61x0.50 inches. In Stock.
-
Mild Differentiability Conditions for Newton\ s Method in Banach Spaces
Verlag: Springer International Publishing, 2020
ISBN 10: 3030487016 ISBN 13: 9783030487010
Sprache: Englisch
Anbieter: moluna, Greven, Deutschland
EUR 52,76
EUR 48,99 für den Versand von Deutschland nach USAAnzahl: Mehr als 20 verfügbar
In den WarenkorbZustand: New.
-
Mild Differentiability Conditions for Newton's Method in Banach Spaces
Verlag: Springer International Publishing, Springer International Publishing Jul 2020, 2020
ISBN 10: 3030487016 ISBN 13: 9783030487010
Sprache: Englisch
Anbieter: buchversandmimpf2000, Emtmannsberg, BAYE, Deutschland
Taschenbuch. Zustand: Neu. Neuware -In this book the authors use a technique based on recurrence relations to study the convergence of the Newton method under mild differentiability conditions on the first derivative of the operator involved. The authors¿ technique relies on the construction of a scalar sequence, not majorizing, that satisfies a system of recurrence relations, and guarantees the convergence of the method. The application is user-friendly and has certain advantages over Kantorovich¿s majorant principle. First, it allows generalizations to be made of the results obtained under conditions of Newton-Kantorovich type and, second, it improves the results obtained through majorizing sequences. In addition, the authors extend the application of Newton¿s method in Banach spaces from the modification of the domain of starting points. As a result, the scope of Kantorovich¿s theory for Newton¿s method is substantially broadened. Moreover, this technique can be applied to any iterative method.This book is chiefly intended for researchers and (postgraduate) students working on nonlinear equations, as well as scientists in general with an interest in numerical analysis.Springer Basel AG in Springer Science + Business Media, Heidelberger Platz 3, 14197 Berlin 192 pp. Englisch.
-
Mild Differentiability Conditions for Newton's Method in Banach Spaces
Verlag: Springer International Publishing, 2020
ISBN 10: 3030487016 ISBN 13: 9783030487010
Sprache: Englisch
Anbieter: AHA-BUCH GmbH, Einbeck, Deutschland
Taschenbuch. Zustand: Neu. Druck auf Anfrage Neuware - Printed after ordering - In this book the authors use a technique based on recurrence relations to study the convergence of the Newton method under mild differentiability conditions on the first derivative of the operator involved. The authors' technique relies on the construction of a scalar sequence, not majorizing, that satisfies a system of recurrence relations, and guarantees the convergence of the method. The application is user-friendly and has certain advantages over Kantorovich's majorant principle. First, it allows generalizations to be made of the results obtained under conditions of Newton-Kantorovich type and, second, it improves the results obtained through majorizing sequences. In addition, the authors extend the application of Newton's method in Banach spaces from the modification of the domain of starting points. As a result, the scope of Kantorovich's theory for Newton's method is substantially broadened. Moreover, this technique can be applied to any iterative method. This book is chiefly intended for researchers and (postgraduate) students working on nonlinear equations, as well as scientists in general with an interest in numerical analysis.
-
Newton's Method: an Updated Approach of Kantorovich's Theory
Verlag: Springer International Publishing, Springer International Publishing Jul 2017, 2017
ISBN 10: 3319559753 ISBN 13: 9783319559759
Sprache: Englisch
Anbieter: buchversandmimpf2000, Emtmannsberg, BAYE, Deutschland
Taschenbuch. Zustand: Neu. Neuware -This book shows the importance of studying semilocal convergence in iterative methods through Newton's method and addresses the most important aspects of the Kantorovich's theory including implicated studies. Kantorovich's theory for Newton's method used techniques of functional analysis to prove the semilocal convergence of the method by means of the well-known majorant principle. To gain a deeper understanding of these techniques the authors return to the beginning and present a deep-detailed approach of Kantorovich's theory for Newton's method, where they include old results, for a historical perspective and for comparisons with new results, refine old results, and prove their most relevant results, where alternative approaches leading to new sufficient semilocal convergence criteria for Newton's method are given. The book contains many numerical examples involving nonlinear integral equations, two boundary value problems and systems of nonlinear equations related to numerous physical phenomena. The book is addressed to researchers in computational sciences, in general, and in approximation of solutions of nonlinear problems, in particular.Springer Basel AG in Springer Science + Business Media, Heidelberger Platz 3, 14197 Berlin 180 pp. Englisch.
-
Convexity in Newton's Method
Verlag: Springer Nature Switzerland, Springer Nature Switzerland, 2025
ISBN 10: 3031857534 ISBN 13: 9783031857539
Sprache: Englisch
Anbieter: AHA-BUCH GmbH, Einbeck, Deutschland
Taschenbuch. Zustand: Neu. Druck auf Anfrage Neuware - Printed after ordering - This monograph examines a variety of iterative methods in Banach spaces with a focus on those obtained from the Newton method. Together with the authors previous two volumes on the topic of the Newton method in Banach spaces, this third volume significantly extends Kantorovich's initial theory. It accomplishes this by emphasizing the influence of the convexity of the function involved, showing how improved iterative methods can be obtained that build upon those introduced in the previous two volumes. Each chapter presents theoretical results and illustrates them with applications to nonlinear equations, including scalar equations, integral equations, boundary value problems, and more. Convexity in Newton's Method will appeal to researchers interested in the theory of the Newton method as well as other iterative methods in Banach spaces.
-
Newton¿s Method: an Updated Approach of Kantorovich¿s Theory
Verlag: Springer International Publishing, Springer International Publishing, 2017
ISBN 10: 3319559753 ISBN 13: 9783319559759
Sprache: Englisch
Anbieter: AHA-BUCH GmbH, Einbeck, Deutschland
Taschenbuch. Zustand: Neu. Druck auf Anfrage Neuware - Printed after ordering - This book shows the importance of studying semilocal convergence in iterative methods through Newton's method and addresses the most important aspects of the Kantorovich's theory including implicated studies. Kantorovich's theory for Newton's method used techniques of functional analysis to prove the semilocal convergence of the method by means of the well-known majorant principle. To gain a deeper understanding of these techniques the authors return to the beginning and present a deep-detailed approach of Kantorovich's theory for Newton's method, where they include old results, for a historical perspective and for comparisons with new results, refine old results, and prove their most relevant results, where alternative approaches leading to new sufficient semilocal convergence criteria for Newton's method are given. The book contains many numerical examples involving nonlinear integral equations, two boundary value problems and systems of nonlinear equations related to numerous physical phenomena. The book is addressed to researchers in computational sciences, in general, and in approximation of solutions of nonlinear problems, in particular.
-
Newton's Method: an Updated Approach of Kantorovich's Theory
Verlag: Springer International Publishing, 2017
ISBN 10: 3319559753 ISBN 13: 9783319559759
Sprache: Englisch
Anbieter: preigu, Osnabrück, Deutschland
Taschenbuch. Zustand: Neu. Newton's Method: an Updated Approach of Kantorovich's Theory | Miguel Ángel Hernández Verón (u. a.) | Taschenbuch | xii | Englisch | 2017 | Springer International Publishing | EAN 9783319559759 | Verantwortliche Person für die EU: Springer Basel AG in Springer Science + Business Media, Heidelberger Platz 3, 14197 Berlin, juergen[dot]hartmann[at]springer[dot]com | Anbieter: preigu.
-
paperback. Zustand: Sehr gut. 256 Seiten; 9783031857539.2 Gewicht in Gramm: 500.